题目分析
本题也是一个经典的单调栈,正好可以巩固一下前几天学习的知识点。
单调栈
我们先看一下样例[3, 1, 2, 4],看一下可以找到什么规律。
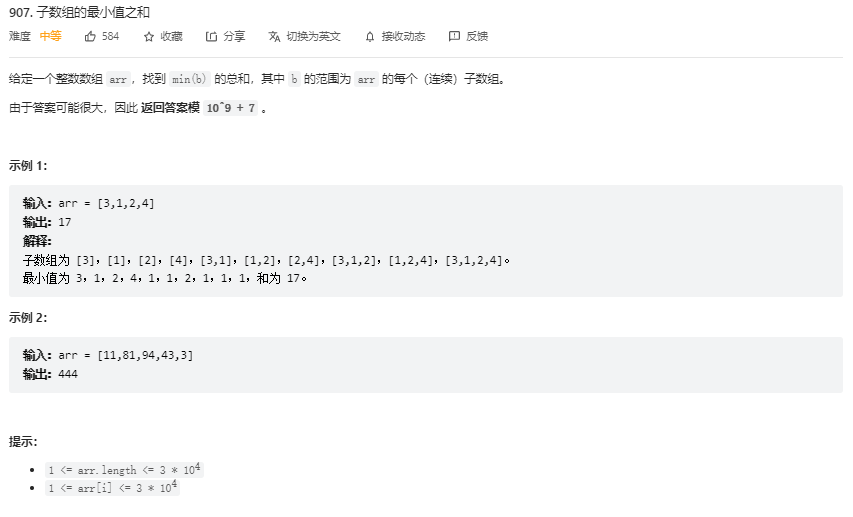
子数组中最小值是3的只有[3]
子数组中最小值是1的有[3, 1], [3, 1, 2], [3, 1, 2, 4], [1], [1, 2], [1, 2, 4]
我们从上面可以看出,最小值是x,说明x的左右都大于等于x。那么就在左侧找到小于x的最晚出现的位置,不妨设到x的距离为m,说明这m个元素(包括x)都是大于等于x的,同理,从右侧找到小于x的最早出现的文章,不妨设到x的距离为n。那么根据乘法原理,从左侧m个元素任选一个作为起点,和右侧n个元素任选一个作为终点,最小值都是x。
我们不妨用上面这个理论检查一下上例中的2和4
子数组中最小值是2的,左边小于2出现的位置是1,与2的距离m = 1,右边所有元素都大于等于2,与2的距离为2,因此子数组应该有2个,[2], [2, 4]。
子数组中最小值是4的,也只有[4]
所以最终的结果是1 x 3 + 6 x 1 + 2 x 2 + 1 x 4 = 17。
如何找小于x最晚的位置呢?这就是单调栈,维护一个单调递增的栈,当栈顶元素大于等于x就弹出,就可以找到小于x的最晚的位置了。同理找到右侧小于x最早的位置,也是维护一个单调递增的栈,只不过是从右向左遍历。
本题还有一个陷阱,就是有重复元素怎么办?统计了左边就不能统计右边了,统计右边就不能统计左边。
如[3, 1, 2, 1],统计第一个1时,左边所有元素都大于等于1,m = 2,右边只能统计到2,不能统计到1。
我们看一下如果统计到1,那么n = 3,就是[3, 1], [3, 1, 2], [3, 1, 2, 1], [1], [1, 2], [1, 2, 1],一共2 x 3 = 6个。
那么计算到第二个1的时候,也按照这个规则,左边所有元素都大于等于1,m = 4, 右边是n = 1,就是[3, 1, 2, 1], [1, 2, 1], [2, 1], [1]。这时就会发现[3, 1, 2, 1]和[1, 2, 1]在前面统计过了。
所以统计左边的时候,寻找小于x的最晚的元素,统计右边的时候,要寻找小于等于x的最早的元素。或者左边寻找小于等于x的最晚的元素,右边寻找小于x最早的元素。
算法的**时间复杂度为O(nlog(n)),空间复杂度为O(n)**。
1 | class Solution { |
刷题总结
这个题目算做中等题也比较坑人,难度比有些hard还要困难。小伙伴们需要多做一些hard题目,现在中等题已经很少出现在面试笔试中了,在大环境不好的情况下,一定要多多刷题,提高自身的能力。